Матрицы

Матрицы и определяемые ими трансформации являются одной из основ трёхмерной графики. В предыдущей статье Вектора, матрицы, трансформации я уже рассказывал о матрицах, но очень поверхностно. Теперь мне бы хотелось детально объяснить вам что такое матрицы, из каких элементов они состоят, что эти элементы значат, привести примеры использования матриц, рассказать об умножении матриц, какие матрицы чаще всего используются в графике и играх и как они выглядят, а так же многое другое. Мне бы хотелось, что бы Вы детально разбирались в операциях над матрицами и могли, в случае необходимости, самостоятельно “собрать” нужную вам матрицу, не прибегая к встроенным функциям DirectX, потому как иногда это бывает нужно.

Умножение на матрицу

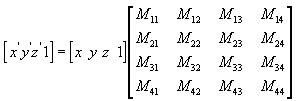Как правило, матрица служит для преобразования вектора. Как я уже говорил в предыдущем уроке, каждая матрица определяет преобразование координат из одной системы координат в другую. Т.е. умножение вектора на матрицу каким-то образом трансформирует вектор, переводя его координаты в другую систему координат. Дабы это Вас не смущало, ещё раз приведу максимально простой пример: считаем центром одной системы координат дверь, а другой системы координат – окно, в этом случае умножив координаты любого предмета, посчитанные относительно двери на матрицу преобразования из системы координат двери в координаты окна, 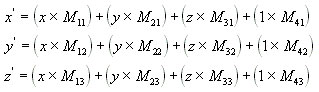мы получим координаты предметы относительно окна (т.е. в системе координат окна). В общем, всё просто. Справа Вы видите полную формулу умножения вектора на матрицу – именно по ней считаются все преобразования, математика уровня 6го класса средней школы )))

Типы матриц

Не следует понимать заголовок этой части текста так, будто есть совершенно разные и особенные типы матриц, которые чем-то совершенно уникальны. Я называю их типами просто для удобства – на самом деле матрица, она и есть матрица и отличаются матрицы лишь значениями их отдельных элементов, не более того. При этом так же надо что бы Вы понимали, что я стараюсь объяснять “на пальцах”, так, что бы понял каждый – с математической точки зрения всё, мягко говоря, несколько сложнее. Я же лишь просто расскажу и покажу то, что Вам нужно знать для того, что бы Вы могли не испытывать особых трудностей с матричной арифметикой и могли понимать как работают преобразования вертексов/моделей/нормалей и т.д. в ваших программах.

Итак, матрицы можно разделить на четыре условных типа:

1. Матрицы сдвига
2. Матрицы вращения
3. Матрицы масштабирования
4. Прочие матрицы (например, перспективные или комбинированные из первых трёх типов)

Матрицы сдвига (Translate Matrix)

Матрицы сдвига это самое простое, что только можно себе представить. Они задают просто “сдвиг” по каждой из осей координат на определённое значение. Этот сдвиг хранится в нижней строке матрицы (в первых трёх её значениях, которые выше обозначены как М₄₁, М₄₂, М₄₃). Если мы зададим в них, например (0, 10, 99), то в результате трансформации любого вектора этой матрицей, он сдвинется на 0 по оси X, на 10 по оси Y и на 99 по оси Z. Мне кажется, совсем не сложно, правда же?

Матрицы масштабирования (Scale Matrix)

Что делают матрицы этого типа, тоже совсем несложно догадаться – они масштабируют. Коэффициенты масштабирования вдоль каждой оси задаются диагональными элементами матриц: М₁₁ для оси X, М₂₂ для оси Y и М₃₃ для оси Z.

Матрицы вращения (Rotate Matrix)

Этот тип матриц несколько сложнее, чем предыдущие. Потому и понять его надо получше, разобраться что к чему и из чего оно следует. Для вращения 2х-мерного вектора, как известно, используется такая формула:

a = угол_поворота;
new_x = old_x*cos(a) - old_y*sin(a)
new_y = old_x*sin(a) + old_y*cos(a)

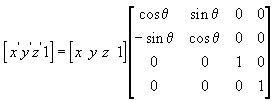А вот так она выглядит в виде матрицы, посмотрите, отличий-то совсем не много… точнее их вообще нет. Поскольку “вращаются” координаты X и Y – само вращение задаётся только в первых 2*2 ячейках. Проще говоря – вращение указывается именно для тех осей, вокруг которых происходит вращение. А оставшаяся, третья, ось (третий столбец + третья строка), остаётся неизменной – там только диагональная единица стоит.

Вот, посмотрите на матрицу вращения вокруг оси X – 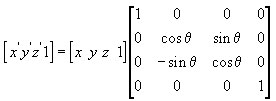Здесь “не используются” (т.е. стоят начальные нули и диагональная единица) первая строка и первый столбец. Надеюсь, я понятно объясняю? Просто посмотрите повнимательнее на картинку и попробуйте споставить с тем, что я говорю. Если Вы это поймёте – у Вас уже никогда больше не возникнет путаницы с матрицами и всё всегда сможете хоть среди ночи с закрытыми глазами правильно написать все три матрицы вращения.

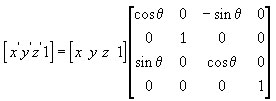Аналогично происходит и с матрицей вращения относительно оси Y. Вы же понимаете о чём я?

Думаю, понимаете. Это же просто. Или это мне так только кажется? Если Вам не понятно – срочно пишите в комментарии и будем разжёвывать дальше, пока не наступит момент полного просветления. Без знания этой темы дальше Вам в компьютерной графике делать просто напросто нечего…

Комбинированные матрицы

Скомбинировать две или более матриц в одну совершенно не проблематично, для этого достаточно просто умножить эти матрицы. Например, если умножить матрицу вращения, масштабирования и сдвига, то умножаемый объект соответственно, повернётся, отмасштабируется, и сдвинется.

Следует понимать, что все трансформации, которые делает матрица над вектором, она делает относительно начала системы координат. Никаких других вариантов просто НЕТ – запомните это!!!! Нельзя, например, повернуть вектор относительно какой-то точки обычной матрицей поворота. Но что же делать, если именно такая задача и стоит? Всё очень просто – надо сделать три матрицы:

1. Матрица сдвига. Такая, что бы точка, вокруг которой будет поворачивать (или вращать) совпала с началом системы координат. Например, если надо сделать трансформацию относительно точки (10, 20, 30), надо сделать матрицу сдвига на (-10, -20, -30)
2. Матрица нужной нам трансформации. В данном случае мы вели речь по поворот, потому матрица поворота
3. Матрица “сдвига на место”, т.е. обратная первой матрице, сдвиг не на (-10, -20, -30), а на (10, 20, 30)

После этого умножить их друг на друга и получить конечную матрицу. И вот она уже будет делать то, что нам и нужно, а именно, вращение вокруг указанной нами точки:

матрица_результирующая = сдвиг * вращение * обратный_сдвиг;

Умножать матрицы умеете? Если нет, вот простое правило: чтобы умножить две матрицы, нужно каждую строку первой матрицы умножить на каждый столбец второй матрицы. Умножая первую строку первой матрицы на каждый столбец второй матрицы мы получим все элементы первой строки матрицы произведения, затем делаем то же самое для второй строки первой матрицы и т.д. Рисунок в данном случае объяснит лучше, чем я:

Я надеюсь, что понятно – не могу придумать, как объяснить лучше.

Умножение матриц не коммутативно

Запомните это раз и навсегда! Т.е. матА*матБ вовсе не обязано быть равно матБ*матА! Это важнейшее правило, не забывайте про него никогда. Объясняю в картинках:

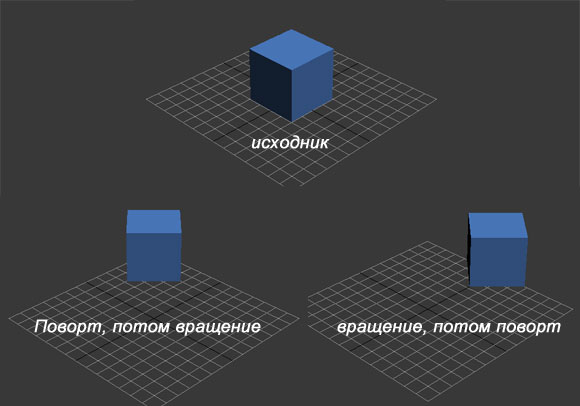
Видите разницу в положении кубов на сетке? От порядка применения матриц зависит конечный результат – об этом надо всегда помнить.

Единичная матрица (матрица идентичности, Identity Matrix)

Единичная матрица это та матрица, которая не производит никаких трансформаций. В ней все нули, а по диагонали единицы.

Примеры применения матриц

Кроме того, что мы можем просто задавать матрицами положение объекта в пространстве, матрицы могут помочь нам и легко связать положение предметов друг к другу. Предположим, что у нас есть некая “база для вентилятора” и есть сам вентилятор (лопасти). Мы можем задать положение и того и другого в мире игры в виде матриц. Но мы можем сделать лучше! Мы можем привязать вентилятор к его “базе”. При этом, во время отрисовки, положение самого вентилятора (лопастей) будет задаваться не только его матрицей, но и матрицей того, к чему он приявзан, т.е. будет считаться так:

матрица_результ = матрица_лопасти * матрица_база

Как итог – если мы начнём трансформировать (двигать, вращать) базу вентилятора – следом за ней будут двигаться и лопасти! Сами! Без какого-либо нашего участия!

Вентиляторы в игре Alien Moon привязаны к базам, что сильно упрощает работу с ними

Тоже не слишком короткий и не особо простой урок получился, однако ) Жду ваших комментариев!!!